- 分享
2028 届选拔考试
- @ 2025-9-12 18:17:29
二分与猜数
二分是解决很多问题的核心思想,在信息学奥赛中被广泛应用。
一个广为人知的问题是: 在 至 里猜一个整数 , 每次问一个整数 ,不能问两次相同的 , 会告诉他 与 的大小关系,直到 猜中为至,问 用什么策略猜最好呢?
答案是, 每次猜 可能存在区间的中间数,那么这个区间每次都会减小一半,比如最开始我们猜 ,那么 要么比 大,要么比 小,要么等于 ,这下 可能存在的区间大小都变成原来的一半,又因为 ,所以最多减半 7 次后, 可能存在的区间都只有 个数,那自然 也就被确定了。
假如问题推广到在 区间,那么容易发现猜的次数是 次的,这里 代表猜的次数的渐进数量级,如:
给 个同学点名的复杂度是 的,给 个同学点名也是 的,给 个同学点名的复杂度的还是 的,因为只要我们多找一个老师同时点,那么每个老师需要点的次数还是不超过 次。而给 个同学点名的复杂度是 的,因为假如你请 个老师点名, 为常数,那么当 时每个老师点名次数依旧超过了 。如果把老师看做计算机单元,点名学生看成计算,那么我们仅仅需要考虑增加计算机单元解决不了的问题。
给出 函数的定义: 。
那么怎么证明这个策略最优呢?我们先定义最优的策略为最大猜到答案次数最小的策略,那么每一次猜测相当于我们把问题分成了两支,就可以画成一个树形图:
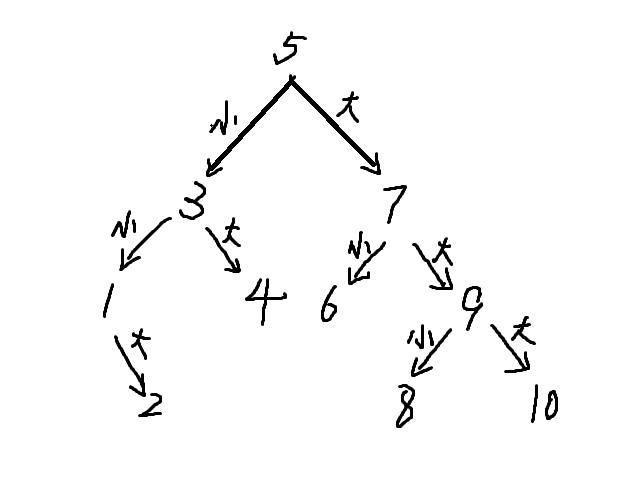
这是一个 时画出的最优决策之一下的树形图。
这样的树叫做决策树,每个决策下一步是两个不同的决策,而一个决策也对应着答案,也就是这一次猜到了的结果,每个点都对应着一个答案。
对于一个猜 里整数的决策树:
-
这个决策树一共有多少个节点?
-
在图中这样的决策方法中,猜哪些数字会导致猜到 的次数最大?
-
构造一个 时最劣决策方式的树形图(即让猜到 最大可能次数最大的决策)。
-
证明决策树至少存在一个需要 次才能猜到的决策。
提示:
第 层的节点个数至多是第 层的两倍。
排序问题:对于 个互不相同的数,把他们从大到小排成一排,请给出尽量快的算法。
二分算法是许多排序算法的核心思想,给出这样一个排序算法:
对于一个长度为 的序列 ,我们每次随机拿出一个数 ,把比 小的数放到 前面,比 大的数放在 后面,那么我们只需要再对比他大的数做一次同样的过程,比他小的数做一次同样的过程,最后一定能得到有序的序列,比如对于序列 :
-
我们选定 当中间那个数,序列变成:。
-
再分别对前一半序列 和后一半 做同样的过程:
-
前一半序列选定 当中间,那么只剩 单个元素一定有序,得到
-
后一半序列选定 当中间,前后都只剩一个元素一定有序,得到
-
那么原序列就变成了 显然有序。
概率论告诉我们每次选的数都靠近中间,所以和上面猜数是本质相同的过程,但因为我们每一次决策都要把数重排,需要 的复杂度,随机下期望有 层,所以在随机下复杂度期望为 。
- 在这种排序算法的启发下,试给出一个求出序列第 大是谁的 算法。
提示: 复杂度为:$O(n+\frac n 2 + \frac n 4 + \frac n 8+ \cdots ) = O(n)$
对于原序列来说,排序结果无非是对原序列标号的重排之一,而原序列共有 $n!=n\times(n-1)\times(n-2)\times\cdots\times 2\times 1$ 种重排,每次比较 和 得到的信息无非是 在 前面或者是 在 的前面两种,那么按照这样可以画出一个类似猜数的决策树,每一种原序列的重排都是决策树的一个终止节点(答案)。
- 试证明基于比较的排序复杂度下界为 。
提示:
位与功能完备
在生活中,加法乘法是最普遍被认识的运算。众所周知,计算机是以二进制的形式存储信息的,正因如此,对于计算机,最基本的运算并非加法或乘法,而是 布尔运算。
就像十进制下的一位上可以是 到 ,二进制下的一位上只会是 或是 ,布尔运算就是对 或 之间进行的运算,下面是几种常见的布尔运算:
- 运算,表示取反:
- 运算,表示取或, 当且仅当 中至少有一个是 ,否则为 :
-
运算,表示取与, 当且仅当 都为 ,否则为 。
-
运算,表示取异或, 当且仅当 不等于 ,否则为 。
- 对于 运算,我们能给出这个运算的真值表如下,请画出 与 的真值表。
我们称一个布尔运算组合是功能完备的,当且仅当这些位运算组合出的新运算就可以构造出全部的布尔运算,如:
$$A \text{ and } B = ((\text{not } A)\text{ or }(\text{not B})) $$是用了 构造了 。
- 请求出有多少本质不同的二元布尔运算,我们称两个二元布尔运算本质不同,当且仅当存在一对 对两个布尔运算的结果是不同的,例:
存在 时,,所以我们称 本质不同。
- 已知 这三种运算的组合可以构造出全部的二元布尔运算,试证明 可以构造出全部的二元布尔运算,其中:
-
试证明 是功能完备的(不考虑 0 元的情况)。
-
试使用 构造出二进制下的整数加法。
开放题:
-
你为什么学习信息学奥赛?
-
你有哪些编程、数学、计算机方面的基础?
-
你迄今为止遇到过最大的问题是什么,你采用了哪些手段解决它?
65 comments
-
 李昕璐 LV 6 @ 2025-10-7 15:53:28
李昕璐 LV 6 @ 2025-10-7 15:53:28有在开放题写小作文的吗,有的话回家看看微信里是不是多了4块钱
-
@ 2025-9-19 20:00:05
#include<bits/stdc++.h> using namespace std; int main() { int a,b; cin>>a>>b; cout<<a/b<<" "<<a%b; return 0; }
🤡 2👀 1 -
 @ 2025-9-12 19:43:16
@ 2025-9-12 19:43:16 -
 @ 2025-9-12 19:42:50
@ 2025-9-12 19:42:50#include <bits/stdc++.h> using namespace std; int main() { cout << "* * * * * " << endl; cout << "* * * * * " << endl; cout << "* * * * * " << endl; cout << "* * * * * " << endl; cout << "* * * * * " << endl; return 0; }
-
 @ 2025-9-12 19:42:24
@ 2025-9-12 19:42:24
-
 @ 2025-9-12 19:42:13
@ 2025-9-12 19:42:13
-
 @ 2025-9-12 19:38:57
@ 2025-9-12 19:38:57一、猜数与决策树决策树总节点数:([n, 2^{\lceil \log_2 n \rceil} - 1])最大猜测次数对应数字:区间端点数字(n=5)最劣决策树:1→2→3→4→5(4、5 需 4 次)证明结论:必存在需(O(\log n))次猜测的数字二、排序与第 k 大第 k 大算法:快速选择算法((O(n)))排序复杂度下界:(O(n\log n))三、布尔运算and 真值表:(0,0)=0,(0,1)=0,(1,0)=0,(1,1)=1 xor 真值表:(0,0)=0,(0,1)=1,(1,0)=1,(1,1)=0二元布尔运算数:16 种nand:功能完备二进制加法:通过 and、or(配合 not)实现本位和与进位逻辑(具体见逻辑表达式)
👍 1 -
 @ 2025-9-12 19:37:15
@ 2025-9-12 19:37:15 👎 3
👎 3 -
 @ 2025-9-12 19:37:10
@ 2025-9-12 19:37:10一、猜数与决策树决策树总节点数:([n, 2^{\lceil \log_2 n \rceil} - 1])最大猜测次数对应数字:区间端点数字(n=5)最劣决策树:1→2→3→4→5(4、5 需 4 次)证明结论:必存在需(O(\log n))次猜测的数字二、排序与第 k 大第 k 大算法:快速选择算法((O(n)))排序复杂度下界:(O(n\log n))三、布尔运算and 真值表:(0,0)=0,(0,1)=0,(1,0)=0,(1,1)=1 xor 真值表:(0,0)=0,(0,1)=1,(1,0)=1,(1,1)=0二元布尔运算数:16 种nand:功能完备二进制加法:通过 and、or(配合 not)实现本位和与进位逻辑(具体见逻辑表达式)
-
 @ 2025-9-12 19:37:03
@ 2025-9-12 19:37:03
-
 @ 2025-9-12 19:36:51
@ 2025-9-12 19:36:51
-
 @ 2025-9-12 19:36:44
@ 2025-9-12 19:36:44 👍 1
👍 1 -
 @ 2025-9-12 19:36:38
@ 2025-9-12 19:36:38
-
 @ 2025-9-12 19:35:58
@ 2025-9-12 19:35:587891 7891 7891 7891 7891 7891 7891 7891 7891 7891 7891 7891 7891 789i 7891 7891 7891 7891 7891 7891 7891 7891 7891 7891 7891 找不同
-
 @ 2025-9-12 19:35:31
@ 2025-9-12 19:35:31
-
 @ 2025-9-12 19:35:24
@ 2025-9-12 19:35:24
-
 @ 2025-9-12 19:34:53
@ 2025-9-12 19:34:53一、猜数问题与决策树分析 在猜 [1,n] 区间内整数的问题中,决策树是核心分析工具,每个节点代表一次猜测,叶子节点代表最终答案(即具体的整数)。以下围绕决策树的关键问题展开解答:
- 决策树的总节点数 决策树是一棵二叉树(每次猜测将问题分为 “猜大”“猜小” 两支,若猜对则为叶子节点)。设树的深度为 d (最大猜测次数,即从根节点到最深叶子节点的路径长度),根据二叉树的性质:
深度为 d 的二叉树,最多能容纳 2 d −1 个节点(等比数列求和: 1+2+2 2 +⋯+2 d−1 =2 d −1 )。 由于需要覆盖 [1,n] 中的所有 n 个整数,叶子节点数至少为 n 。而深度为 d 的二叉树,最多有 2 d−1
个叶子节点(根节点在第 1 层,第 d 层为叶子节点),因此 2 d−1 ≥n ,即 d≥⌈log 2 n⌉ 。
此时决策树的总节点数需满足:至少覆盖 n 个叶子节点,因此总节点数范围为 [n,2 ⌈log 2 n⌉ −1] 。例如:
当 n=5 时, ⌈log 2 5⌉=3 ,总节点数最多为 2 3 −1=7 ,最少为 5(极端情况下为 “链状” 树,但最优策略下为平衡二叉树)。 2. 最大猜测次数对应的数字 最优决策树是平衡二叉树(每次猜测尽可能将区间均分,使最大深度最小)。此时:
最大猜测次数对应的数字是决策树中最深叶子节点对应的整数,即 “区间均分后,无法再均分的边界数字”。
例如:
当 n=10 时,最优策略的决策树(平衡二叉树)如下: 第 1 次猜 5(将 [1,10] 分为 [1,4] 和 [6,10]); 第 2 次猜 2([1,4] 分 [1,1] 和 [3,4])或 8([6,10] 分 [6,7] 和 [9,10]); 第 3 次猜 1/3/4/6/7/9/10(其中 1、4、6、10 需 3 次猜测,为最大次数)。
结论:平衡决策树中,区间的 “端点数字”(如 1、n、均分后的子区间端点)通常需要最大猜测次数。 3. n=5 时的最劣决策树(最大次数最大) 最劣决策树的目标是 “让某一数字的猜测次数尽可能大”,即构造一棵极度不平衡的二叉树(每次猜测仅排除一个数字,而非均分区间)。
构造过程(以 “每次猜最小数” 为例):
根节点(第 1 次猜):1 → 若对则结束(1 次);若错(答案在 [2,5]),进入右子树。 第 2 次猜:2 → 若对则结束(2 次);若错(答案在 [3,5]),进入右子树。 第 3 次猜:3 → 若对则结束(3 次);若错(答案在 [4,5]),进入右子树。 第 4 次猜:4 → 若对则结束(4 次);若错则答案为 5(4 次)。
对应的树形图(文字表示):
plaintext 1 (第1次)
2 (第2次)
3 (第3次)
4 (第4次)
5 (第4次)此时,数字 4 和 5 需 4 次猜测,是最大次数(最劣情况)。 4. 证明决策树至少存在一个数字需 O(logn) 次猜测 采用反证法,结合二叉树的节点数性质:
假设所有数字的猜测次数都小于 log 2 n ,即最大深度 d<log 2 n (取整数则 d≤⌊log 2 n⌋−1 )。 根据二叉树叶子节点数上限:深度为 d 的二叉树,最多有 2 d
个叶子节点(根在第 1 层,第 d+1 层为叶子)。 若 d<log 2 n ,则 2 d <n ,即叶子节点数 < n ,无法覆盖 [1,n] 中的所有 n 个整数,矛盾。
因此,必然存在至少一个数字,其猜测次数 ≥ ⌈log 2 n⌉ ,即次数为 O(logn) 。 二、排序算法相关问题 排序的核心是 “比较元素大小并确定顺序”,以下围绕 “基于比较的排序复杂度下界” 和 “快速选择算法” 展开。
- 求序列第 k 大的 O(n) 算法(快速选择算法) 基于 “快速排序的分治思想”,无需完整排序即可找到第 k 大元素,步骤如下:
选择基准元素:从序列中随机选一个元素 pivot ; 分区操作:将序列分为三部分: 左区:比 pivot 大的元素(目标是找第 k 大,故按 “大→小” 分区); 中区:等于 pivot 的元素; 右区:比 pivot 小的元素; 判断 pivot 的位置: 若左区元素个数 L>k−1 :第 k 大元素在左区,递归处理左区; 若 中 区 个 数 : pivot 就是第 k 大元素,直接返回; 若 中 区 个 数 :第 k 大元素在右区,递归处理右区(此时需找右区的第 中 区 个 数 大元素)。
复杂度分析:
每次分区操作需遍历当前序列,复杂度 O(m) ( m 为当前序列长度); 由于随机选择 pivot ,平均情况下每次分区会将序列分为 “大致相等” 的两部分,递归深度为 O(logn) ,但每次处理的序列长度递减: n→n/2→n/4→… ; 总复杂度: O(n+n/2+n/4+…)=O(n) (等比数列求和,首项 n ,公比 1/2 ,和为 2n )。 2. 证明基于比较的排序复杂度下界为 O(nlogn) 基于 “决策树模型”,每个排序算法对应一棵二叉决策树,节点含义如下:
内部节点:一次元素比较(如比较 a i
和 a j
); 叶子节点:一个 “排序结果”(即 n 个元素的一种排列,共 n! 种可能)。
关键推理步骤:
决策树的深度与复杂度:排序的时间复杂度 = 决策树的最大深度(即最坏情况下的比较次数)。 叶子节点数的约束:由于排序结果有 n! 种,决策树的叶子节点数 ≥ n! 。 二叉树的深度约束:深度为 d 的二叉树,最多有 2 d
个叶子节点(根在第 1 层,第 d+1 层为叶子)。因此: 2 d ≥n!⟹d≥log 2 (n!) 化简 log 2 (n!) :根据斯特林公式( n!≈n n e −n
2πn
),取对数得: log 2 (n!)≈log 2 (n n e −n
2πn )=nlog 2 n−nlog 2 e+ 2 1 log 2 (2πn)
当 n 足够大时,主导项为 nlog 2 n ,即 log 2 (n!)=O(nlogn) 。
因此,基于比较的排序算法,最坏情况下的复杂度下界为 O(nlogn) 。 三、布尔运算相关问题 布尔运算以 0/1 为输入,共 4 种二元布尔运算(输入组合:(0,0),(0,1),(1,0),(1,1)),以下围绕真值表、功能完备性展开。
- and 与 xor 的真值表 二元布尔运算的输入组合固定为 4 种,根据运算定义可得真值表:
A B A and B A xor B 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0
and 运算:仅当 A、B 均为 1 时输出 1,否则为 0; xor 运算:当 A、B 不同时输出 1,相同时输出 0(“异或”)。 2. 本质不同的二元布尔运算数量 二元布尔运算的输入有 4 种组合,每种组合的输出可独立为 0 或 1,因此总共有 2 4 =16 种本质不同的二元布尔运算。
可按输出结果的 “1 的个数” 分类(共 5 类):
0 个 1:恒假运算(输出全 0); 1 个 1:仅 (1,1) 输出 1(即 and 运算)、仅 (1,0) 输出 1(A 且 not B)、仅 (0,1) 输出 1(not A 且 B)、仅 (0,0) 输出 1(恒假的反); 2 个 1:xor 运算((0,1),(1,0) 输出 1)、or 运算((0,1),(1,0),(1,1) 输出 1 的反?不,or 是 3 个 1)、等价运算((0,0),(1,1) 输出 1,xor 的反)等; 3 个 1:or 运算(仅 (0,0) 输出 0)、nand 运算的反等; 4 个 1:恒真运算(输出全 1)。
综上,本质不同的二元布尔运算共 16 种。 3. 证明 nand 运算功能完备(不考虑 0 元运算) 功能完备性的定义:仅用该运算可构造出所有布尔运算(not、and、or、xor 等)。nand 运算定义为 A nand B=not(A and B) ,证明步骤如下:
用 nand 构造 not 运算: 令 B = A,则 A nand A=not(A and A)=not A (因为 A and A=A )。 例: 1 nand 1=not(1 and 1)=0=not 1 ; 0 nand 0=1=not 0 。 用 nand 构造 and 运算: 根据 nand 定义, A and B=not(A nand B) 。 而 not 可由 nand 构造,因此: A and B=(A nand B) nand (A nand B) 。 用 nand 构造 or 运算: 根据德摩根定律, A or B=not(not A and not B) 。 代入 nand 定义: not A and not B=(not A) nand (not B) 的反,因此: A or B=(not A) nand (not B)
再用 nand 表示 not: not A=A nand A ,故: A or B=(A nand A) nand (B nand B) 用 nand 构造 xor 运算: xor 可表示为 A xor B=(A or B) and not(A and B) 。 由于 or、and、not 均能由 nand 构造,因此 xor 也可由 nand 构造。
综上,nand 可构造出所有布尔运算,nand 是功能完备的。 4. 用 and、or 构造二进制整数加法 二进制加法需考虑 “本位和” 与 “进位”,设两个 1 位二进制数为 A、B,低位进位为 C_in,本位和为 S,高位进位为 C_out。
1 位加法的逻辑表达式: 本位和 S:仅当 A、B、C_in 中有奇数个 1 时为 1,即 S=(A xor B) xor C i n ; 进位 C_out:当 A、B、C_in 中有至少两个 1 时为 1,即 C o ut=(A and B) or (A and C i n) or (B and C i n) 。 用 and、or 表示 xor: xor 可通过 and、or、not 表示(德摩根定律): A xor B=(A or B) and not(A and B)
若允许使用 not(注:题目未禁止 not,且 and/or 常与 not 配合使用;若严格仅用 and/or,需通过 “补码” 隐含 not,但实际加法需 not),则可代入 S 的表达式。 多位加法的扩展: 对于 n 位二进制数 A = A n−1 …A 1 A 0
、B = B n−1 …B 1 B 0
,从最低位(0 位)开始,依次计算每一位的 S 和 C_out,将 C_out 作为下一位的 C_in,最高位的 C_out 为最终进位(若有)。
示例(2 位二进制加法:A=10,B=01):
0 位:A=0,B=1,C_in=0 → S=1,C_out=0; 1 位:A=1,B=0,C_in=0 → S=1,C_out=0; 结果:S=11(即十进制 3),符合 2+1=3。
综上,通过 and、or(配合 not)可构造二进制加法的 “本位和” 答案是啥 以下是你所提问题的核心答案汇总,按模块整理,便于快速查阅: 一、猜数问题与决策树 决策树总节点数 范围为 [n,2 ⌈log 2 n⌉ −1] 。本质是二叉树需覆盖 n 个叶子节点(对应 [1,n] 整数),深度 d≥⌈log 2 n⌉ ,总节点数上限为等比数列和 2 d −1 。 最大猜测次数对应的数字 最优决策树(平衡二叉树)中,区间端点数字(如 1、n、均分后的子区间端点,例 n=10 时的 1、4、6、10)需最大猜测次数。 n=5 最劣决策树 构造极度不平衡二叉树(每次猜最小数),树形为:1(第 1 次)→2(第 2 次)→3(第 3 次)→4(第 4 次)→5(第 4 次),数字 4、5 需 4 次猜测(最大次数)。 证明存在需 O (logn) 次的数字 反证法:若所有数字次数 < log₂n,则决策树深度 d<log 2 n ,叶子节点数 ≤ 2ᵈ <n,无法覆盖 [1,n],矛盾。故必存在数字需 ⌈log 2 n⌉=O(logn) 次。 二、排序与第 k 大算法 求第 k 大的 O (n) 算法(快速选择) 步骤:随机选 pivot → 按 “比 pivot 大 / 小” 分区 → 若左区 size > k-1,递归左区;若左区 + 中区 size ≥k,返回 pivot;否则递归右区(找第 k - 左区 - 中区大)。 复杂度: O(n+n/2+n/4+...)=O(n) 。 基于比较的排序复杂度下界 O (nlogn) 排序对应二叉决策树,叶子节点数 ≥ n!(n 个元素的排列数)。 深度 d≥log 2 (n!) ,由斯特林公式 n!≈n n e −n
2πn
,得 log 2 (n!)=O(nlogn) ,故下界为 O (nlogn)。 三、布尔运算 and/xor 真值表 A B A and B A xor B 0 0 0 0 0 1 0 1 1 0 0 1 1 1 1 0 本质不同的二元布尔运算数 共 16 种(4 种输入组合,每种输出 0/1 独立, 2 4 =16 )。 nand 功能完备性证明 构造 not: notA=A nand A ; 构造 and: AandB=(AnandB) nand (AnandB) ; 构造 or: AorB=(AnandA) nand (BnandB) ; 可进一步构造 xor 等,故 nand 功能完备。 and/or 构造二进制加法 1 位加法:本位和 S=[(AorB)and not(AandB)] xor C in
(xor 用 and/or/not 表示),进位 C out =(AandB)or(AandC in )or(BandC in ) ; 多位加法:从低位到高位,依次传递进位,叠加每一位和。 直接说答案 一、猜数与决策树 决策树总节点数: [n,2 ⌈log 2 n⌉ −1] 最大猜测次数对应数字:区间端点(如 n=10 时 1、4、6、10) n=5 最劣决策树:1→2→3→4→5(4、5 需 4 次) 证明:反证法,若均 < log 2 n 次,叶子数 < n 矛盾,故必存 O(logn) 次的数 二、排序与第 k 大 第 k 大算法:快速选择(随机选 pivot 分区,递归找对应区间,复杂度 O(n) ) 排序下界: O(nlogn) (决策树叶子≥ n! , log 2 (n!)=O(nlogn) ) 三、布尔运算 and/xor 真值表:如上表(A=1,B=1 时 and=1、xor=0;A=0,B=1 时 and=0、xor=1) 二元布尔运算数:16 种 nand 完备性:可构造 not(A nand A)、and、or,故完备 二进制加法:1 位 S=(A⊕B)⊕C_in,C_out=(A&B)∨(A&C_in)∨(B&C_in)(⊕用 and/or/not 表示),多位递推进位
❤️ 2 -
 @ 2025-9-12 19:33:58
@ 2025-9-12 19:33:58
-
 @ 2025-9-12 19:33:51
@ 2025-9-12 19:33:51
-
 @ 2025-9-12 19:33:44
@ 2025-9-12 19:33:44
-
 @ 2025-9-12 19:33:33
@ 2025-9-12 19:33:33
-
 @ 2025-9-12 19:32:45
@ 2025-9-12 19:32:45威龙无敌
-
@ 2025-9-12 19:32:34
54188 741 741 7878
-
 @ 2025-9-12 19:32:22
@ 2025-9-12 19:32:22
-
 @ 2025-9-12 19:32:10
@ 2025-9-12 19:32:10
-
 @ 2025-9-12 19:31:58
@ 2025-9-12 19:31:58直接查答案不就行了
-
@ 2025-9-12 19:31:20
741 741
-
 @ 2025-9-12 19:31:04
@ 2025-9-12 19:31:04_1. n n。
每个决策点本身对应一个答案,共 n n 种答案,所以有 n n 个点。
_2.
2 , 8 , 10 2,8,10。
每个决策点深度对应其答案猜到的次数,所以答案是最深的三个点
_3. 从 1 1 猜到 10 10 或者从 10 10 猜到 1 1 都可以。
分别当 x
10 x=10, x
1 x=1 时猜到次数为 n n 次,取到上限。
_4. 证:
第 k k 层最多有 2 k − 1 2 k−1 个点,假设每一层都取满,至少取 k k 层,那么有:
1 + 2 1 + 2 2 + ⋯ + 2 k − 1 ≥ n 1+2 1 +2 2 +⋯+2 k−1 ≥n 根据提示,有:
2 k − 1 ≥ n 2 k −1≥n 那么 k
O ( log n ) k=O(logn),至少有 O ( log n ) O(logn) 层,所以最劣情况下至少要猜 O ( log n ) O(logn) 次。
_5.
考虑给出排序算法的过程,我们每次能确定选出的中间的数的排名为他左边数 a c a c 的个数 + 1 +1,那么我们就能确定第 k k 大比 a c a c 大还是比 a c a c 小,只需要处理包含第 k k 大的左区间或者右区间,期望每次这个区间长度除以 2 2,所以根据提示,复杂度:
O ( n + n 2 + n 4 + . . . )
O ( n ) O(n+ 2 n + 4 n +...)=O(n) 易证这个算法最优,因为读取一遍 a a 数组都需要 O ( n ) O(n)。
_6.
考虑重排能构造出的决策树,如果某个决策点所经过的所有决策进行的比较能确定出一个重排 p p,那么他一定不会再继续进行决策,那么他一定是一个叶子节点。
一共有 n ! n! 个重排,每个对应一个叶子,算法的复杂度即为决策树最深点的深度,那么假设我们有一个算法让决策树变成满二叉树,那这个算法的复杂度一定最优。
假设最深的层数即答案是 k k,那么有 2 k − 1
n ! 2 k−1 =n!, k
O ( log n ! ) k=O(logn!),根据提示, k
O ( n log n ) k=O(nlogn),我们就证明了基于比较的排序复杂度下限为 O ( n log n ) O(nlogn)。
怎么证明提示呢?
2 log n !
log ( n ! ) 2 2logn!=log(n!) 2
那么交换一下有:
( n ! ) 2
∏ i
1 n i ( n − i + 1 ) (n!) 2
i=1 ∏ n i(n−i+1) 而 min i
1 n i ( n − i + 1 )
n min i=1 n i(n−i+1)=n,则 ( n ! ) 2
n n (n!) 2
n n .
根据 log log 的单调性,有:
log n ! < log n n < 2 log n ! logn!<logn n <2logn! 则: O ( log n ! )
O ( n log n ) O(logn!)=O(nlogn).
位与功能完备 _1.
A B A and B 0 0 0 0 1 0 1 0 0 1 1 1 A 0 0 1 1
B 0 1 0 1
A and B 0 0 0 1
A B A xor B 0 0 0 0 1 1 1 0 1 1 1 0 A 0 0 1 1
B 0 1 0 1
A xor B 0 1 1 0
_2. 16
我们发现一个从二元布尔运算和真值表是双射的,那么我们对真值表计数即可: A , B A,B 共有 2 2 2 2 种选法,每种 A opt B A opt B 有两种选法,所以有 2 2 2
16 2 2 2
=16 种真值表,即有 16 16 种不同的二元布尔运算。
_3. 证明:
可以用 nand nand 构造 {not, and, or} {not, and, or}:
not A
A nand A not A=A nand A A and B
not ( A nand B ) A and B =not (A nand B) A or B
( not A ) and ( not B ) A or B=(not A) and (not B) 逐步代入即可,不需要化简。
而 {not, and, or} {not, and, or} 能构造出所有二元布尔运算,所以 nand nand 也可以。
_4.
考虑一个 k ( k ≥ 3 ) k(k≥3) 元布尔运算和 k k 元真值表双射,而对于一个真值表,我们考虑如何用二元布尔函数构造出其对应的布尔运算。
对于真值表对应的 k k 元运算 o p t ( x 1 , x 2 , . . . , x k ) opt(x 1 ,x 2 ,...,x k ),假设真值表第 c c 行 x i
k c i x i =k ci ,结果为 o c o c ,则当 x x 的取值方案与其中一个 o c
1 o c =1 的行相同时运算的结果为 1 1,容易写出 x x 的取值方法为 k c k c 的判断式:
and i
1 k
k c i xnor x i and i=1 k k ci xnor x i
其中, A xnor B
1 A xnor B=1 当且仅当 A
B A=B。
那么对于所有 o c
1 o c =1 的行,和其中一行的取值相等即可,有:
o p t ( x 1 , x 2 , . . . , x k )
or o c
1 ( and i
1 k
k c i xnor x i ) opt(x 1 ,x 2 ,...,x k )=or o c =1 (and i=1 k k ci xnor x i ) 再把 nand nand 构造出的各个二元运算代换掉即可。
👀 1🌿 1 -
 @ 2025-9-12 19:30:27
@ 2025-9-12 19:30:27今日运势 § 小吉 § 已连续打卡 1 天,累计打卡 1 天
😄 1 -
@ 2025-9-12 19:29:58
54188
-
 @ 2025-9-12 19:29:52
@ 2025-9-12 19:29:52
-
@ 2025-9-12 19:29:30
,wdjkie gfjeltrmjkljljol
-
@ 2025-9-12 19:29:05
iouhik6rdimjtnoworjtl6tfk,ykjyrmj kclrfynhn5te
-
@ 2025-9-12 19:29:01
#include <bits/stdc++.h> using namespace std; int main() { int a,b,c; cin>>a>>b>>c; if(a>=b&&a>=c) { cout<<a; } else { if(a<c) { cout<<c; } else { cout<<b; } } }
-
@ 2025-9-12 19:28:57

-
@ 2025-9-12 19:28:54
hdtrmjghitrofhimjw5yioyjhk4tgfk3
-
@ 2025-9-12 19:28:41
ti5rujhw8iyju5yh4
-
 @ 2025-9-12 19:28:36
@ 2025-9-12 19:28:36二分与猜数
二分是解决很多问题的核心思想,在信息学奥赛中被广泛应用。
一个广为人知的问题是: A A 在 1 1 至 100 100 里猜一个整数 x x, B B 每次问一个整数 y y,不能问两次相同的 y y, A A 会告诉他 x x 与 y y 的大小关系,直到 B B 猜中为至,问 B B 用什么策略猜最好呢?
答案是, B B 每次猜 x x 可能存在区间的中间数,那么这个区间每次都会减小一半,比如最开始我们猜 y
50 y=50,那么 x x 要么比 50 50 大,要么比 50 50 小,要么等于 50 50,这下 x x 可能存在的区间大小都变成原来的一半,又因为 2 6 < 100 < 2 7 2 6 <100<2 7 ,所以最多减半 7 次后, x x 可能存在的区间都只有 1 1 个数,那自然 x x 也就被确定了。
假如问题推广到在 [ 1 , n ] [1,n] 区间,那么容易发现猜的次数是 O ( log n ) O(logn) 次的,这里 O ( log n ) O(logn) 代表猜的次数的渐进数量级,如:
给 n n 个同学点名的复杂度是 O ( n ) O(n) 的,给 ( n + 1 ) (n+1) 个同学点名也是 O ( n ) O(n) 的,给 2 n 2n 个同学点名的复杂度的还是 O ( n ) O(n) 的,因为只要我们多找一个老师同时点,那么每个老师需要点的次数还是不超过 n n 次。而给 n 2 n 2 个同学点名的复杂度是 O ( n ) O(n) 的,因为假如你请 k k 个老师点名, k k 为常数,那么当 n
k + 1 n=k+1 时每个老师点名次数依旧超过了 n n。如果把老师看做计算机单元,点名学生看成计算,那么我们仅仅需要考虑增加计算机单元解决不了的问题。
给出 log log 函数的定义: 2 log x
x 2 logx =x。
那么怎么证明这个策略最优呢?我们先定义最优的策略为最大猜到答案次数最小的策略,那么每一次猜测相当于我们把问题分成了两支,就可以画成一个树形图:
这是一个 n
10 n=10 时画出的最优决策之一下的树形图。
这样的树叫做决策树,每个决策下一步是两个不同的决策,而一个决策也对应着答案,也就是这一次猜到了的结果,每个点都对应着一个答案。
对于一个猜 [ 1 , n ] [1,n] 里整数的决策树:
这个决策树一共有多少个节点?
在图中这样的决策方法中,猜哪些数字会导致猜到 x x 的次数最大?
构造一个 n
5 n=5 时最劣决策方式的树形图(即让猜到 x x 最大可能次数最大的决策)。
证明决策树至少存在一个需要 O ( log n ) O(logn) 次才能猜到的决策。
提示:
1 + 2 1 + 2 2 + ⋯ + 2 n
2 n + 1 − 1 1+2 1 +2 2 +⋯+2 n =2 n+1 −1 第 i i 层的节点个数至多是第 ( i − 1 ) (i−1) 层的两倍。
排序问题:对于 n n 个互不相同的数,把他们从大到小排成一排,请给出尽量快的算法。
二分算法是许多排序算法的核心思想,给出这样一个排序算法:
对于一个长度为 n n 的序列 a n a n ,我们每次随机拿出一个数 a x a x ,把比 a x a x 小的数放到 a x a x 前面,比 a x a x 大的数放在 a x a x 后面,那么我们只需要再对比他大的数做一次同样的过程,比他小的数做一次同样的过程,最后一定能得到有序的序列,比如对于序列 { 4 , 3 , 2 , 1 , 6 , 5 } {4,3,2,1,6,5}:
我们选定 3 3 当中间那个数,序列变成: { 2 , 1 , 3 , 4 , 6 , 5 } {2,1,3,4,6,5}。
再分别对前一半序列 { 2 , 1 } {2,1} 和后一半 { 4 , 6 , 5 } {4,6,5} 做同样的过程:
前一半序列选定 2 2 当中间,那么只剩 { 1 } {1} 单个元素一定有序,得到 { 1 , 2 } {1,2}
后一半序列选定 5 5 当中间,前后都只剩一个元素一定有序,得到 { 4 , 5 , 6 } {4,5,6}
那么原序列就变成了 { 1 , 2 , 3 , 4 , 5 , 6 } {1,2,3,4,5,6} 显然有序。
概率论告诉我们每次选的数都靠近中间,所以和上面猜数是本质相同的过程,但因为我们每一次决策都要把数重排,需要 O ( n ) O(n) 的复杂度,随机下期望有 O ( log n ) O(logn) 层,所以在随机下复杂度期望为 O ( n ) × O ( log n )
O ( n log n ) O(n)×O(logn)=O(nlogn)。
在这种排序算法的启发下,试给出一个求出序列第 k k 大是谁的 O ( n ) O(n) 算法。 提示: 复杂度为: O ( n + n 2 + n 4 + n 8 + ⋯ )
O ( n ) O(n+ 2 n + 4 n + 8 n +⋯)=O(n)
对于原序列来说,排序结果无非是对原序列标号的重排之一,而原序列共有 n !
n × ( n − 1 ) × ( n − 2 ) × ⋯ × 2 × 1 n!=n×(n−1)×(n−2)×⋯×2×1 种重排,每次比较 a i a i 和 a j a j 得到的信息无非是 a i a i 在 a j a j 前面或者是 a j a j 在 a i a i 的前面两种,那么按照这样可以画出一个类似猜数的决策树,每一种原序列的重排都是决策树的一个终止节点(答案)。
试证明基于比较的排序复杂度下界为 O ( n log n ) O(nlogn)。 提示: O ( log n ! )
O ( n log n ) O(logn!)=O(nlogn)
位与功能完备
在生活中,加法乘法是最普遍被认识的运算。众所周知,计算机是以二进制的形式存储信息的,正因如此,对于计算机,最基本的运算并非加法或乘法,而是 布尔运算。
就像十进制下的一位上可以是 0 0 到 9 9,二进制下的一位上只会是 0 0 或是 1 1,布尔运算就是对 0 0 或 1 1 之间进行的运算,下面是几种常见的布尔运算:
not not 运算,表示取反: not 1
0 not 1=0 not 0
1 not 0=1 or or 运算,表示取或, a or b
1 a or b=1 当且仅当 a , b a,b 中至少有一个是 1 1,否则为 0 0: 1 or 0
0 or 1
1 or 1
1 1 or 0=0 or 1=1 or 1=1 0 or 0
0 0 or 0=0 and and 运算,表示取与, A and B
1 A and B=1 当且仅当 a , b a,b 都为 1 1,否则为 0 0。
xor xor 运算,表示取异或, A xor B
1 A xor B=1 当且仅当 a a 不等于 b b,否则为 0 0。
对于 or or 运算,我们能给出这个运算的真值表如下,请画出 and and 与 xor xor 的真值表。 A B A or B 0 0 0 0 1 1 1 0 1 1 1 1 A 0 0 1 1
B 0 1 0 1
A or B 0 1 1 1
我们称一个布尔运算组合是功能完备的,当且仅当这些位运算组合出的新运算就可以构造出全部的布尔运算,如:
A and B
( ( not A ) or ( not B ) ) A and B=((not A) or (not B)) 是用了 not, or not, or 构造了 and and。
请求出有多少本质不同的二元布尔运算,我们称两个二元布尔运算本质不同,当且仅当存在一对 ( A , B ) (A,B) 对两个布尔运算的结果是不同的,例: 存在 A
1 , B
0 A=1,B=0 时, A and B ≠ A or B A and B =A or B,所以我们称 and, or and, or 本质不同。
已知 (not, and, or) (not, and, or) 这三种运算的组合可以构造出全部的二元布尔运算,试证明 nand nand 可以构造出全部的二元布尔运算,其中: A nand B
not ( A and B ) A nand B=not (A and B) 试证明 nand nand 是功能完备的(不考虑 0 元的情况)。
试使用 and, or and, or 构造出二进制下的整数加法。
开放题:
你为什么学习信息学奥赛?
你有哪些编程、数学、计算机方面的基础?
你迄今为止遇到过最大的问题是什么,你采用了哪些手段解决它?
-
 @ 2025-9-12 19:28:24
@ 2025-9-12 19:28:24二分与猜数
二分是解决很多问题的核心思想,在信息学奥赛中被广泛应用。
一个广为人知的问题是: A A 在 1 1 至 100 100 里猜一个整数 x x, B B 每次问一个整数 y y,不能问两次相同的 y y, A A 会告诉他 x x 与 y y 的大小关系,直到 B B 猜中为至,问 B B 用什么策略猜最好呢?
答案是, B B 每次猜 x x 可能存在区间的中间数,那么这个区间每次都会减小一半,比如最开始我们猜 y
50 y=50,那么 x x 要么比 50 50 大,要么比 50 50 小,要么等于 50 50,这下 x x 可能存在的区间大小都变成原来的一半,又因为 2 6 < 100 < 2 7 2 6 <100<2 7 ,所以最多减半 7 次后, x x 可能存在的区间都只有 1 1 个数,那自然 x x 也就被确定了。
假如问题推广到在 [ 1 , n ] [1,n] 区间,那么容易发现猜的次数是 O ( log n ) O(logn) 次的,这里 O ( log n ) O(logn) 代表猜的次数的渐进数量级,如:
给 n n 个同学点名的复杂度是 O ( n ) O(n) 的,给 ( n + 1 ) (n+1) 个同学点名也是 O ( n ) O(n) 的,给 2 n 2n 个同学点名的复杂度的还是 O ( n ) O(n) 的,因为只要我们多找一个老师同时点,那么每个老师需要点的次数还是不超过 n n 次。而给 n 2 n 2 个同学点名的复杂度是 O ( n ) O(n) 的,因为假如你请 k k 个老师点名, k k 为常数,那么当 n
k + 1 n=k+1 时每个老师点名次数依旧超过了 n n。如果把老师看做计算机单元,点名学生看成计算,那么我们仅仅需要考虑增加计算机单元解决不了的问题。
给出 log log 函数的定义: 2 log x
x 2 logx =x。
那么怎么证明这个策略最优呢?我们先定义最优的策略为最大猜到答案次数最小的策略,那么每一次猜测相当于我们把问题分成了两支,就可以画成一个树形图:
这是一个 n
10 n=10 时画出的最优决策之一下的树形图。
这样的树叫做决策树,每个决策下一步是两个不同的决策,而一个决策也对应着答案,也就是这一次猜到了的结果,每个点都对应着一个答案。
对于一个猜 [ 1 , n ] [1,n] 里整数的决策树:
这个决策树一共有多少个节点?
在图中这样的决策方法中,猜哪些数字会导致猜到 x x 的次数最大?
构造一个 n
5 n=5 时最劣决策方式的树形图(即让猜到 x x 最大可能次数最大的决策)。
证明决策树至少存在一个需要 O ( log n ) O(logn) 次才能猜到的决策。
提示:
1 + 2 1 + 2 2 + ⋯ + 2 n
2 n + 1 − 1 1+2 1 +2 2 +⋯+2 n =2 n+1 −1 第 i i 层的节点个数至多是第 ( i − 1 ) (i−1) 层的两倍。
排序问题:对于 n n 个互不相同的数,把他们从大到小排成一排,请给出尽量快的算法。
二分算法是许多排序算法的核心思想,给出这样一个排序算法:
对于一个长度为 n n 的序列 a n a n ,我们每次随机拿出一个数 a x a x ,把比 a x a x 小的数放到 a x a x 前面,比 a x a x 大的数放在 a x a x 后面,那么我们只需要再对比他大的数做一次同样的过程,比他小的数做一次同样的过程,最后一定能得到有序的序列,比如对于序列 { 4 , 3 , 2 , 1 , 6 , 5 } {4,3,2,1,6,5}:
我们选定 3 3 当中间那个数,序列变成: { 2 , 1 , 3 , 4 , 6 , 5 } {2,1,3,4,6,5}。
再分别对前一半序列 { 2 , 1 } {2,1} 和后一半 { 4 , 6 , 5 } {4,6,5} 做同样的过程:
前一半序列选定 2 2 当中间,那么只剩 { 1 } {1} 单个元素一定有序,得到 { 1 , 2 } {1,2}
后一半序列选定 5 5 当中间,前后都只剩一个元素一定有序,得到 { 4 , 5 , 6 } {4,5,6}
那么原序列就变成了 { 1 , 2 , 3 , 4 , 5 , 6 } {1,2,3,4,5,6} 显然有序。
概率论告诉我们每次选的数都靠近中间,所以和上面猜数是本质相同的过程,但因为我们每一次决策都要把数重排,需要 O ( n ) O(n) 的复杂度,随机下期望有 O ( log n ) O(logn) 层,所以在随机下复杂度期望为 O ( n ) × O ( log n )
O ( n log n ) O(n)×O(logn)=O(nlogn)。
在这种排序算法的启发下,试给出一个求出序列第 k k 大是谁的 O ( n ) O(n) 算法。 提示: 复杂度为: O ( n + n 2 + n 4 + n 8 + ⋯ )
O ( n ) O(n+ 2 n + 4 n + 8 n +⋯)=O(n)
对于原序列来说,排序结果无非是对原序列标号的重排之一,而原序列共有 n !
n × ( n − 1 ) × ( n − 2 ) × ⋯ × 2 × 1 n!=n×(n−1)×(n−2)×⋯×2×1 种重排,每次比较 a i a i 和 a j a j 得到的信息无非是 a i a i 在 a j a j 前面或者是 a j a j 在 a i a i 的前面两种,那么按照这样可以画出一个类似猜数的决策树,每一种原序列的重排都是决策树的一个终止节点(答案)。
试证明基于比较的排序复杂度下界为 O ( n log n ) O(nlogn)。 提示: O ( log n ! )
O ( n log n ) O(logn!)=O(nlogn)
位与功能完备
在生活中,加法乘法是最普遍被认识的运算。众所周知,计算机是以二进制的形式存储信息的,正因如此,对于计算机,最基本的运算并非加法或乘法,而是 布尔运算。
就像十进制下的一位上可以是 0 0 到 9 9,二进制下的一位上只会是 0 0 或是 1 1,布尔运算就是对 0 0 或 1 1 之间进行的运算,下面是几种常见的布尔运算:
not not 运算,表示取反: not 1
0 not 1=0 not 0
1 not 0=1 or or 运算,表示取或, a or b
1 a or b=1 当且仅当 a , b a,b 中至少有一个是 1 1,否则为 0 0: 1 or 0
0 or 1
1 or 1
1 1 or 0=0 or 1=1 or 1=1 0 or 0
0 0 or 0=0 and and 运算,表示取与, A and B
1 A and B=1 当且仅当 a , b a,b 都为 1 1,否则为 0 0。
xor xor 运算,表示取异或, A xor B
1 A xor B=1 当且仅当 a a 不等于 b b,否则为 0 0。
对于 or or 运算,我们能给出这个运算的真值表如下,请画出 and and 与 xor xor 的真值表。 A B A or B 0 0 0 0 1 1 1 0 1 1 1 1 A 0 0 1 1
B 0 1 0 1
A or B 0 1 1 1
我们称一个布尔运算组合是功能完备的,当且仅当这些位运算组合出的新运算就可以构造出全部的布尔运算,如:
A and B
( ( not A ) or ( not B ) ) A and B=((not A) or (not B)) 是用了 not, or not, or 构造了 and and。
请求出有多少本质不同的二元布尔运算,我们称两个二元布尔运算本质不同,当且仅当存在一对 ( A , B ) (A,B) 对两个布尔运算的结果是不同的,例: 存在 A
1 , B
0 A=1,B=0 时, A and B ≠ A or B A and B =A or B,所以我们称 and, or and, or 本质不同。
已知 (not, and, or) (not, and, or) 这三种运算的组合可以构造出全部的二元布尔运算,试证明 nand nand 可以构造出全部的二元布尔运算,其中: A nand B
not ( A and B ) A nand B=not (A and B) 试证明 nand nand 是功能完备的(不考虑 0 元的情况)。
试使用 and, or and, or 构造出二进制下的整数加法。
开放题:
你为什么学习信息学奥赛?
你有哪些编程、数学、计算机方面的基础?
你迄今为止遇到过最大的问题是什么,你采用了哪些手段解决它?
-
 @ 2025-9-12 19:28:15
@ 2025-9-12 19:28:15二分与猜数
二分是解决很多问题的核心思想,在信息学奥赛中被广泛应用。
一个广为人知的问题是: A A 在 1 1 至 100 100 里猜一个整数 x x, B B 每次问一个整数 y y,不能问两次相同的 y y, A A 会告诉他 x x 与 y y 的大小关系,直到 B B 猜中为至,问 B B 用什么策略猜最好呢?
答案是, B B 每次猜 x x 可能存在区间的中间数,那么这个区间每次都会减小一半,比如最开始我们猜 y
50 y=50,那么 x x 要么比 50 50 大,要么比 50 50 小,要么等于 50 50,这下 x x 可能存在的区间大小都变成原来的一半,又因为 2 6 < 100 < 2 7 2 6 <100<2 7 ,所以最多减半 7 次后, x x 可能存在的区间都只有 1 1 个数,那自然 x x 也就被确定了。
假如问题推广到在 [ 1 , n ] [1,n] 区间,那么容易发现猜的次数是 O ( log n ) O(logn) 次的,这里 O ( log n ) O(logn) 代表猜的次数的渐进数量级,如:
给 n n 个同学点名的复杂度是 O ( n ) O(n) 的,给 ( n + 1 ) (n+1) 个同学点名也是 O ( n ) O(n) 的,给 2 n 2n 个同学点名的复杂度的还是 O ( n ) O(n) 的,因为只要我们多找一个老师同时点,那么每个老师需要点的次数还是不超过 n n 次。而给 n 2 n 2 个同学点名的复杂度是 O ( n ) O(n) 的,因为假如你请 k k 个老师点名, k k 为常数,那么当 n
k + 1 n=k+1 时每个老师点名次数依旧超过了 n n。如果把老师看做计算机单元,点名学生看成计算,那么我们仅仅需要考虑增加计算机单元解决不了的问题。
给出 log log 函数的定义: 2 log x
x 2 logx =x。
那么怎么证明这个策略最优呢?我们先定义最优的策略为最大猜到答案次数最小的策略,那么每一次猜测相当于我们把问题分成了两支,就可以画成一个树形图:
这是一个 n
10 n=10 时画出的最优决策之一下的树形图。
这样的树叫做决策树,每个决策下一步是两个不同的决策,而一个决策也对应着答案,也就是这一次猜到了的结果,每个点都对应着一个答案。
对于一个猜 [ 1 , n ] [1,n] 里整数的决策树:
这个决策树一共有多少个节点?
在图中这样的决策方法中,猜哪些数字会导致猜到 x x 的次数最大?
构造一个 n
5 n=5 时最劣决策方式的树形图(即让猜到 x x 最大可能次数最大的决策)。
证明决策树至少存在一个需要 O ( log n ) O(logn) 次才能猜到的决策。
提示:
1 + 2 1 + 2 2 + ⋯ + 2 n
2 n + 1 − 1 1+2 1 +2 2 +⋯+2 n =2 n+1 −1 第 i i 层的节点个数至多是第 ( i − 1 ) (i−1) 层的两倍。
排序问题:对于 n n 个互不相同的数,把他们从大到小排成一排,请给出尽量快的算法。
二分算法是许多排序算法的核心思想,给出这样一个排序算法:
对于一个长度为 n n 的序列 a n a n ,我们每次随机拿出一个数 a x a x ,把比 a x a x 小的数放到 a x a x 前面,比 a x a x 大的数放在 a x a x 后面,那么我们只需要再对比他大的数做一次同样的过程,比他小的数做一次同样的过程,最后一定能得到有序的序列,比如对于序列 { 4 , 3 , 2 , 1 , 6 , 5 } {4,3,2,1,6,5}:
我们选定 3 3 当中间那个数,序列变成: { 2 , 1 , 3 , 4 , 6 , 5 } {2,1,3,4,6,5}。
再分别对前一半序列 { 2 , 1 } {2,1} 和后一半 { 4 , 6 , 5 } {4,6,5} 做同样的过程:
前一半序列选定 2 2 当中间,那么只剩 { 1 } {1} 单个元素一定有序,得到 { 1 , 2 } {1,2}
后一半序列选定 5 5 当中间,前后都只剩一个元素一定有序,得到 { 4 , 5 , 6 } {4,5,6}
那么原序列就变成了 { 1 , 2 , 3 , 4 , 5 , 6 } {1,2,3,4,5,6} 显然有序。
概率论告诉我们每次选的数都靠近中间,所以和上面猜数是本质相同的过程,但因为我们每一次决策都要把数重排,需要 O ( n ) O(n) 的复杂度,随机下期望有 O ( log n ) O(logn) 层,所以在随机下复杂度期望为 O ( n ) × O ( log n )
O ( n log n ) O(n)×O(logn)=O(nlogn)。
在这种排序算法的启发下,试给出一个求出序列第 k k 大是谁的 O ( n ) O(n) 算法。 提示: 复杂度为: O ( n + n 2 + n 4 + n 8 + ⋯ )
O ( n ) O(n+ 2 n + 4 n + 8 n +⋯)=O(n)
对于原序列来说,排序结果无非是对原序列标号的重排之一,而原序列共有 n !
n × ( n − 1 ) × ( n − 2 ) × ⋯ × 2 × 1 n!=n×(n−1)×(n−2)×⋯×2×1 种重排,每次比较 a i a i 和 a j a j 得到的信息无非是 a i a i 在 a j a j 前面或者是 a j a j 在 a i a i 的前面两种,那么按照这样可以画出一个类似猜数的决策树,每一种原序列的重排都是决策树的一个终止节点(答案)。
试证明基于比较的排序复杂度下界为 O ( n log n ) O(nlogn)。 提示: O ( log n ! )
O ( n log n ) O(logn!)=O(nlogn)
位与功能完备
在生活中,加法乘法是最普遍被认识的运算。众所周知,计算机是以二进制的形式存储信息的,正因如此,对于计算机,最基本的运算并非加法或乘法,而是 布尔运算。
就像十进制下的一位上可以是 0 0 到 9 9,二进制下的一位上只会是 0 0 或是 1 1,布尔运算就是对 0 0 或 1 1 之间进行的运算,下面是几种常见的布尔运算:
not not 运算,表示取反: not 1
0 not 1=0 not 0
1 not 0=1 or or 运算,表示取或, a or b
1 a or b=1 当且仅当 a , b a,b 中至少有一个是 1 1,否则为 0 0: 1 or 0
0 or 1
1 or 1
1 1 or 0=0 or 1=1 or 1=1 0 or 0
0 0 or 0=0 and and 运算,表示取与, A and B
1 A and B=1 当且仅当 a , b a,b 都为 1 1,否则为 0 0。
xor xor 运算,表示取异或, A xor B
1 A xor B=1 当且仅当 a a 不等于 b b,否则为 0 0。
对于 or or 运算,我们能给出这个运算的真值表如下,请画出 and and 与 xor xor 的真值表。 A B A or B 0 0 0 0 1 1 1 0 1 1 1 1 A 0 0 1 1
B 0 1 0 1
A or B 0 1 1 1
我们称一个布尔运算组合是功能完备的,当且仅当这些位运算组合出的新运算就可以构造出全部的布尔运算,如:
A and B
( ( not A ) or ( not B ) ) A and B=((not A) or (not B)) 是用了 not, or not, or 构造了 and and。
请求出有多少本质不同的二元布尔运算,我们称两个二元布尔运算本质不同,当且仅当存在一对 ( A , B ) (A,B) 对两个布尔运算的结果是不同的,例: 存在 A
1 , B
0 A=1,B=0 时, A and B ≠ A or B A and B =A or B,所以我们称 and, or and, or 本质不同。
已知 (not, and, or) (not, and, or) 这三种运算的组合可以构造出全部的二元布尔运算,试证明 nand nand 可以构造出全部的二元布尔运算,其中: A nand B
not ( A and B ) A nand B=not (A and B) 试证明 nand nand 是功能完备的(不考虑 0 元的情况)。
试使用 and, or and, or 构造出二进制下的整数加法。
开放题:
你为什么学习信息学奥赛?
你有哪些编程、数学、计算机方面的基础?
你迄今为止遇到过最大的问题是什么,你采用了哪些手段解决它?
-
 @ 2025-9-12 19:28:02
@ 2025-9-12 19:28:02谁叫我周子铁
-
@ 2025-9-12 19:27:43
e
-
@ 2025-9-12 19:27:37
drdygfyhgbujwopejgf8wegji
-
@ 2025-9-12 19:26:06
谁发的暗区突围😐
-
@ 2025-9-12 19:24:39
****t43rqwf r4sy42qgre5rweg54~gwey34gheway4> g~wfrtgy4tt34t43tgewhyweaghewghwegewh34`ggweg34ywaeh4rtwe```ehfdstesrftgweryers~~wtehe3wrfwey34t~yt32gersy23tf34y32~ gwerh5tewy5436y65y3f4tj68orj87tfe53hft5iuytg4e67uihyi65$t5rjsetgy54etjtrfgrgh54wr###### ewt643hrwar3265weg437rqw5t132r4yurewekjlhewjkfghvhbhjgfkjvbljkfoijlksdjflkasjdfpiowsdjflksajfpoias;iodpugoiwehtgkjehgiukhw,edfjioeuwgh5tgkwiaegyu9ierhyjelrytrheisyhuerh45hwaruehrhhtjh$
`rty45ttr4 -
 @ 2025-9-12 19:24:11
@ 2025-9-12 19:24:11二分与猜数
二分是解决很多问题的核心思想,在信息学奥赛中被广泛应用。
一个广为人知的问题是: A A 在 1 1 至 100 100 里猜一个整数 x x, B B 每次问一个整数 y y,不能问两次相同的 y y, A A 会告诉他 x x 与 y y 的大小关系,直到 B B 猜中为至,问 B B 用什么策略猜最好呢?
答案是, B B 每次猜 x x 可能存在区间的中间数,那么这个区间每次都会减小一半,比如最开始我们猜 y
50 y=50,那么 x x 要么比 50 50 大,要么比 50 50 小,要么等于 50 50,这下 x x 可能存在的区间大小都变成原来的一半,又因为 2 6 < 100 < 2 7 2 6 <100<2 7 ,所以最多减半 7 次后, x x 可能存在的区间都只有 1 1 个数,那自然 x x 也就被确定了。
假如问题推广到在 [ 1 , n ] [1,n] 区间,那么容易发现猜的次数是 O ( log n ) O(logn) 次的,这里 O ( log n ) O(logn) 代表猜的次数的渐进数量级,如:
给 n n 个同学点名的复杂度是 O ( n ) O(n) 的,给 ( n + 1 ) (n+1) 个同学点名也是 O ( n ) O(n) 的,给 2 n 2n 个同学点名的复杂度的还是 O ( n ) O(n) 的,因为只要我们多找一个老师同时点,那么每个老师需要点的次数还是不超过 n n 次。而给 n 2 n 2 个同学点名的复杂度是 O ( n ) O(n) 的,因为假如你请 k k 个老师点名, k k 为常数,那么当 n
k + 1 n=k+1 时每个老师点名次数依旧超过了 n n。如果把老师看做计算机单元,点名学生看成计算,那么我们仅仅需要考虑增加计算机单元解决不了的问题。
给出 log log 函数的定义: 2 log x
x 2 logx =x。
那么怎么证明这个策略最优呢?我们先定义最优的策略为最大猜到答案次数最小的策略,那么每一次猜测相当于我们把问题分成了两支,就可以画成一个树形图:
这是一个 n
10 n=10 时画出的最优决策之一下的树形图。
这样的树叫做决策树,每个决策下一步是两个不同的决策,而一个决策也对应着答案,也就是这一次猜到了的结果,每个点都对应着一个答案。
对于一个猜 [ 1 , n ] [1,n] 里整数的决策树:
这个决策树一共有多少个节点?
在图中这样的决策方法中,猜哪些数字会导致猜到 x x 的次数最大?
构造一个 n
5 n=5 时最劣决策方式的树形图(即让猜到 x x 最大可能次数最大的决策)。
证明决策树至少存在一个需要 O ( log n ) O(logn) 次才能猜到的决策。
提示:
1 + 2 1 + 2 2 + ⋯ + 2 n
2 n + 1 − 1 1+2 1 +2 2 +⋯+2 n =2 n+1 −1 第 i i 层的节点个数至多是第 ( i − 1 ) (i−1) 层的两倍。
排序问题:对于 n n 个互不相同的数,把他们从大到小排成一排,请给出尽量快的算法。
二分算法是许多排序算法的核心思想,给出这样一个排序算法:
对于一个长度为 n n 的序列 a n a n ,我们每次随机拿出一个数 a x a x ,把比 a x a x 小的数放到 a x a x 前面,比 a x a x 大的数放在 a x a x 后面,那么我们只需要再对比他大的数做一次同样的过程,比他小的数做一次同样的过程,最后一定能得到有序的序列,比如对于序列 { 4 , 3 , 2 , 1 , 6 , 5 } {4,3,2,1,6,5}:
我们选定 3 3 当中间那个数,序列变成: { 2 , 1 , 3 , 4 , 6 , 5 } {2,1,3,4,6,5}。
再分别对前一半序列 { 2 , 1 } {2,1} 和后一半 { 4 , 6 , 5 } {4,6,5} 做同样的过程:
前一半序列选定 2 2 当中间,那么只剩 { 1 } {1} 单个元素一定有序,得到 { 1 , 2 } {1,2}
后一半序列选定 5 5 当中间,前后都只剩一个元素一定有序,得到 { 4 , 5 , 6 } {4,5,6}
那么原序列就变成了 { 1 , 2 , 3 , 4 , 5 , 6 } {1,2,3,4,5,6} 显然有序。
概率论告诉我们每次选的数都靠近中间,所以和上面猜数是本质相同的过程,但因为我们每一次决策都要把数重排,需要 O ( n ) O(n) 的复杂度,随机下期望有 O ( log n ) O(logn) 层,所以在随机下复杂度期望为 O ( n ) × O ( log n )
O ( n log n ) O(n)×O(logn)=O(nlogn)。
在这种排序算法的启发下,试给出一个求出序列第 k k 大是谁的 O ( n ) O(n) 算法。 提示: 复杂度为: O ( n + n 2 + n 4 + n 8 + ⋯ )
O ( n ) O(n+ 2 n + 4 n + 8 n +⋯)=O(n)
对于原序列来说,排序结果无非是对原序列标号的重排之一,而原序列共有 n !
n × ( n − 1 ) × ( n − 2 ) × ⋯ × 2 × 1 n!=n×(n−1)×(n−2)×⋯×2×1 种重排,每次比较 a i a i 和 a j a j 得到的信息无非是 a i a i 在 a j a j 前面或者是 a j a j 在 a i a i 的前面两种,那么按照这样可以画出一个类似猜数的决策树,每一种原序列的重排都是决策树的一个终止节点(答案)。
试证明基于比较的排序复杂度下界为 O ( n log n ) O(nlogn)。 提示: O ( log n ! )
O ( n log n ) O(logn!)=O(nlogn)
位与功能完备
在生活中,加法乘法是最普遍被认识的运算。众所周知,计算机是以二进制的形式存储信息的,正因如此,对于计算机,最基本的运算并非加法或乘法,而是 布尔运算。
就像十进制下的一位上可以是 0 0 到 9 9,二进制下的一位上只会是 0 0 或是 1 1,布尔运算就是对 0 0 或 1 1 之间进行的运算,下面是几种常见的布尔运算:
not not 运算,表示取反: not 1
0 not 1=0 not 0
1 not 0=1 or or 运算,表示取或, a or b
1 a or b=1 当且仅当 a , b a,b 中至少有一个是 1 1,否则为 0 0: 1 or 0
0 or 1
1 or 1
1 1 or 0=0 or 1=1 or 1=1 0 or 0
0 0 or 0=0 and and 运算,表示取与, A and B
1 A and B=1 当且仅当 a , b a,b 都为 1 1,否则为 0 0。
xor xor 运算,表示取异或, A xor B
1 A xor B=1 当且仅当 a a 不等于 b b,否则为 0 0。
对于 or or 运算,我们能给出这个运算的真值表如下,请画出 and and 与 xor xor 的真值表。 A B A or B 0 0 0 0 1 1 1 0 1 1 1 1 A 0 0 1 1
B 0 1 0 1
A or B 0 1 1 1
我们称一个布尔运算组合是功能完备的,当且仅当这些位运算组合出的新运算就可以构造出全部的布尔运算,如:
A and B
( ( not A ) or ( not B ) ) A and B=((not A) or (not B)) 是用了 not, or not, or 构造了 and and。
请求出有多少本质不同的二元布尔运算,我们称两个二元布尔运算本质不同,当且仅当存在一对 ( A , B ) (A,B) 对两个布尔运算的结果是不同的,例: 存在 A
1 , B
0 A=1,B=0 时, A and B ≠ A or B A and B =A or B,所以我们称 and, or and, or 本质不同。
已知 (not, and, or) (not, and, or) 这三种运算的组合可以构造出全部的二元布尔运算,试证明 nand nand 可以构造出全部的二元布尔运算,其中: A nand B
not ( A and B ) A nand B=not (A and B) 试证明 nand nand 是功能完备的(不考虑 0 元的情况)。
试使用 and, or and, or 构造出二进制下的整数加法。
开放题:
你为什么学习信息学奥赛?
你有哪些编程、数学、计算机方面的基础?
你迄今为止遇到过最大的问题是什么,你采用了哪些手段解决它?
-
@ 2025-9-12 19:23:57
foo.cc:2:45: error: extended character ‘ is not valid in an identifier 2 | hfiufjfuimcijfiru./,.,..,.uifh rgirugijmuci/‘plkfoipdfkgvij;p[.d;oecpi | ^ foo.cc:1:1: error: 'whjiejfirejfvnuierwlcnv' does not name a type 1 | whjiejfirejfvnuierwlcnv | ^~~~~~~~~~~~~~~~~~~~~~~ foo.cc:2:61: error: 'p' does not name a type 2 | hfiufjfuimcijfiru./,.,..,.uifh rgirugijmuci/‘plkfoipdfkgvij;p[.d;oecpi | ^ foo.cc:2:66: error: 'oecpi' does not name a type 2 | hfiufjfuimcijfiru./,.,..,.uifh rgirugijmuci/‘plkfoipdfkgvij;p[.d;oecpi | foo.cc:2:45: error: extended character ‘ is not valid in an identifier 2 | hfiufjfuimcijfiru./,.,..,.uifh rgirugijmuci/‘plkfoipdfkgvij;p[.d;oecpi | ^ foo.cc:1:1: error: 'whjiejfirejfvnuierwlcnv' does not name a type 1 | whjiejfirejfvnuierwlcnv | ^~~~~~~~~~~~~~~~~~~~~~~ foo.cc:2:61: error: 'p' does not name a type 2 | hfiufjfuimcijfiru./,.,..,.uifh rgirugijmuci/‘plkfoipdfkgvij;p[.d;oecpi | ^ foo.cc:2:66: error: 'oecpi' does not name a type 2 | hfiufjfuimcijfiru./,.,..,.uifh rgirugijmuci/‘plkfoipdfkgvij;p[.d;oecpi |
-
 @ 2025-9-12 19:23:35
@ 2025-9-12 19:23:356666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666
-
@ 2025-9-12 19:23:29
foo.cc:2:45: error: extended character ‘ is not valid in an identifier 2 | hfiufjfuimcijfiru./,.,..,.uifh rgirugijmuci/‘plkfoipdfkgvij;p[.d;oecpi | ^ foo.cc:1:1: error: 'whjiejfirejfvnuierwlcnv' does not name a type 1 | whjiejfirejfvnuierwlcnv | ^~~~~~~~~~~~~~~~~~~~~~~ foo.cc:2:61: error: 'p' does not name a type 2 | hfiufjfuimcijfiru./,.,..,.uifh rgirugijmuci/‘plkfoipdfkgvij;p[.d;oecpi | ^ foo.cc:2:66: error: 'oecpi' does not name a type 2 | hfiufjfuimcijfiru./,.,..,.uifh rgirugijmuci/‘plkfoipdfkgvij;p[.d;oecpi |
-
 @ 2025-9-12 19:23:16
@ 2025-9-12 19:23:16
