二分与猜数

二分是解决很多问题的核心思想，在信息学奥赛中被广泛应用。

一个广为人知的问题是：$A$ 在 $1$ 至 $100$ 里猜一个整数 $x$，$B$ 每次问一个整数 $y$，不能问两次相同的 $y$，$A$ 会告诉他 $x$ 与 $y$ 的大小关系，直到 $B$ 猜中为至，问 $B$ 用什么策略猜最好呢？

答案是，$B$ 每次猜 $x$ 可能存在区间的中间数，那么这个区间每次都会减小一半，比如最开始我们猜 $y=50$，那么 $x$ 要么比 $50$ 大，要么比 $50$ 小，要么等于 $50$，这下 $x$ 可能存在的区间大小都变成原来的一半，又因为 $2^6 < 100 < 2^7$，所以最多减半 7 次后，$x$ 可能存在的区间都只有 $1$ 个数，那自然 $x$ 也就被确定了。

假如问题推广到在 $[1,n]$ 区间，那么容易发现猜的次数是 $O(\log n)$ 次的，这里 $O(\log n)$ 代表猜的次数的渐进数量级，如：

给 $n$ 个同学点名的复杂度是 $O(n)$ 的，给 $(n+1)$ 个同学点名也是 $O(n)$ 的，给 $2n$ 个同学点名的复杂度的还是 $O(n)$ 的，因为只要我们多找一个老师同时点，那么每个老师需要点的次数还是不超过 $n$ 次。而给 $n^2$ 个同学点名的复杂度是 $O(n)$ 的，因为假如你请 $k$ 个老师点名，$k$ 为常数，那么当 $n=k+1$ 时每个老师点名次数依旧超过了 $n$。如果把老师看做计算机单元，点名学生看成计算，那么我们仅仅需要考虑增加计算机单元解决不了的问题。

给出 $\log$ 函数的定义： $2^{\log x} = x$。

那么怎么证明这个策略最优呢？我们先定义最优的策略为最大猜到答案次数最小的策略，那么每一次猜测相当于我们把问题分成了两支，就可以画成一个树形图：

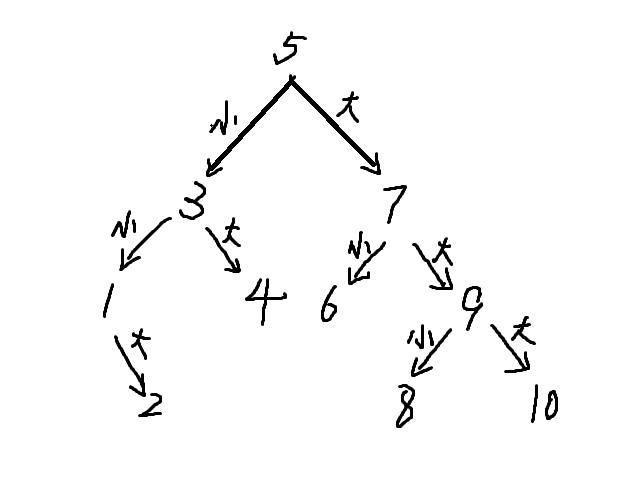
这是一个 $n=10$ 时画出的最优决策之一下的树形图。

这样的树叫做决策树，每个决策下一步是两个不同的决策，而一个决策也对应着答案，也就是这一次猜到了的结果，每个点都对应着一个答案。

对于一个猜 $[1,n]$ 里整数的决策树：

1. 这个决策树一共有多少个节点？

2. 在图中这样的决策方法中，猜哪些数字会导致猜到 $x$ 的次数最大？

3. 构造一个 $n=5$ 时最劣决策方式的树形图（即让猜到 $x$ 最大可能次数最大的决策）。

4. 证明决策树至少存在一个需要 $O(\log n)$ 次才能猜到的决策。

提示：

$$1+2^1 +2^2 + \cdots + 2^n = 2^{n+1} - 1$$

第 $i$ 层的节点个数至多是第 $(i-1)$ 层的两倍。

排序问题：对于 $n$ 个互不相同的数，把他们从大到小排成一排，请给出尽量快的算法。

二分算法是许多排序算法的核心思想，给出这样一个排序算法：

对于一个长度为 $n$ 的序列 $a_n$，我们每次随机拿出一个数 $a_x$，把比 $a_x$ 小的数放到 $a_x$ 前面，比 $a_x$ 大的数放在 $a_x$ 后面，那么我们只需要再对比他大的数做一次同样的过程，比他小的数做一次同样的过程，最后一定能得到有序的序列，比如对于序列 $\{4,3,2,1,6,5\}$：

• 我们选定 $3$ 当中间那个数，序列变成：$\{2,1,3,4,6,5\}$。

• 再分别对前一半序列 $\{2,1\}$ 和后一半 $\{4,6,5\}$ 做同样的过程：

• 前一半序列选定 $2$ 当中间，那么只剩 $\{1\}$ 单个元素一定有序，得到 $\{1,2\}$

• 后一半序列选定 $5$ 当中间，前后都只剩一个元素一定有序，得到 $\{4,5,6\}$

• 那么原序列就变成了 $\{1,2,3,4,5,6\}$ 显然有序。

概率论告诉我们每次选的数都靠近中间，所以和上面猜数是本质相同的过程，但因为我们每一次决策都要把数重排，需要 $O(n)$ 的复杂度，随机下期望有 $O(\log n )$ 层，所以在随机下复杂度期望为 $O(n) \times O(\log n) = O(n\log n)$。

5. 在这种排序算法的启发下，试给出一个求出序列第 $k$ 大是谁的 $O(n)$ 算法。

提示： 复杂度为：$O(n+\frac n 2 + \frac n 4 + \frac n 8+ \cdots ) = O(n)$

对于原序列来说，排序结果无非是对原序列标号的重排之一，而原序列共有 $n!=n\times(n-1)\times(n-2)\times\cdots\times 2\times 1$ 种重排，每次比较 $a_i$ 和 $a_j$ 得到的信息无非是 $a_i$ 在 $a_j$ 前面或者是 $a_j$ 在 $a_i$ 的前面两种，那么按照这样可以画出一个类似猜数的决策树，每一种原序列的重排都是决策树的一个终止节点（答案）。

6. 试证明基于比较的排序复杂度下界为 $O(n\log n)$。

提示：$O(\log n! ) = O(n\log n)$

位与功能完备

在生活中，加法乘法是最普遍被认识的运算。众所周知，计算机是以二进制的形式存储信息的，正因如此，对于计算机，最基本的运算并非加法或乘法，而是 布尔运算。

就像十进制下的一位上可以是 $0$ 到 $9$，二进制下的一位上只会是 $0$ 或是 $1$，布尔运算就是对 $0$ 或 $1$ 之间进行的运算，下面是几种常见的布尔运算：

• $\text {not}$ 运算，表示取反：

$$\text {not } 1 = 0$$ $$\text {not } 0 = 1$$

• $\texttt {or}$ 运算，表示取或，$a \text{ or }b = 1$ 当且仅当 $a,b$ 中至少有一个是 $1$，否则为 $0$：

$$1\text{ or } 0 = 0 \text{ or } 1 = 1 \text{ or } 1 = 1 $$$$0 \text{ or }0=0$$

• $\text{and}$ 运算，表示取与，$A \text{ and } B = 1$ 当且仅当 $a,b$ 都为 $1$，否则为 $0$。

• $\text{xor}$ 运算，表示取异或，$A \text{ xor } B = 1$ 当且仅当 $a$ 不等于 $b$，否则为 $0$。

1. 对于 $\text{or}$ 运算，我们能给出这个运算的真值表如下，请画出 $\text{and}$ 与 $\text{xor}$ 的真值表。

$$\begin{array}{|c|c|c|} \hline A & B & A \text{ or } B \\ \hline 0 & 0 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\ \hline \end{array} $$

我们称一个布尔运算组合是功能完备的，当且仅当这些位运算组合出的新运算就可以构造出全部的布尔运算，如：

$$A \text{ and } B = ((\text{not } A)\text{ or }(\text{not B})) $$

是用了 $\text{not, or}$ 构造了 $\text{and}$。

2. 请求出有多少本质不同的二元布尔运算，我们称两个二元布尔运算本质不同，当且仅当存在一对 $(A,B)$ 对两个布尔运算的结果是不同的，例：

存在 $A=1,B=0$ 时，$A\text{ and }B \neq A \text{ or } B$，所以我们称 $\text{and, or}$ 本质不同。

3. 已知 $\text{(not, and, or)}$ 这三种运算的组合可以构造出全部的二元布尔运算，试证明 $\text{nand}$ 可以构造出全部的二元布尔运算，其中：

$$\text{A nand B}= \text{not }(A \text{ and }B)$$

4. 试证明 $\text{nand}$ 是功能完备的（不考虑 0 元的情况）。

5. 试使用 $\text{and, or}$ 构造出二进制下的整数加法。

开放题：

1. 你为什么学习信息学奥赛？

2. 你有哪些编程、数学、计算机方面的基础？

3. 你迄今为止遇到过最大的问题是什么，你采用了哪些手段解决它？